3d Equi-Angular Spiral Generator a ObjectARX® MFC application for AutoCAD® for Autodesk's AutoCAD® versions 2000 to 2017, x32/x64bit.

Create a 3d Equi-Angular Spiral PolyFace Mesh in AutoCAD®
r = exp(theta * cotan a)
Background Photo:   NGC 628 - Messier No. 74, Gemini North Observatory - GMOS Team, August 13-14, 2001
Appload the ObjectARX application, type DRAWSPIRAL at the Command Prompt,
Which activates this modal dialog, Set the Parameters, and Click OK.
Parameters:
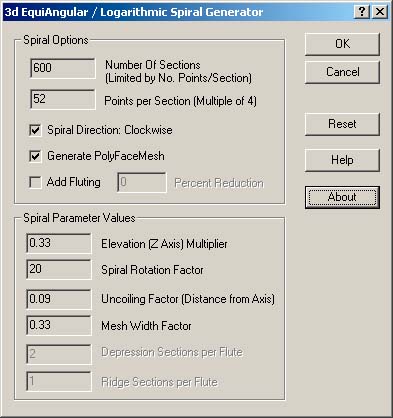
Number of Sections:
A PolyFaceMesh in AutoCAD is limited to 32676 vertices (the value of a short int). You'll need to keep the product of the Number of Sections times the Number of Points Per Section below this value. Dialog defaults are set close to that maximum value. The valid range for this number is from 2 to 1000.
Number of Points Per Section:
Due to the way the mesh is calculated, the Number of Points Per Section has to be entered as number that is divisible by 4. If it's not, after selecting OK, the program will change it, and possibly the previous value of the Number of Sections for suitability. The valid range for this number is from 8 to 100.
Spiral Direction:
Use this check box to alter the spiral direction from Clockwise, to Counterclockwise.
Generate A PolyFaceMesh:
Use this check box to generate either a PolyFaceMesh, and a centered 3d Polyline, or only the single 3d Polyline. Note that if the Z elevation is 0, a 2d Polyline is created instead of a 3d Polyline.
Add Fluting:
Use this check box to modify the PolyFaceMesh using the parameters in the Percent Reduction, Ridge Sections per Flute, and Depression Sections per Flute text fields. The mesh reduction is applied continuously along the specified number of depression sections of the PolyFaceMesh. The default is to not adjust the mesh.
Percent Reduction:
The numeric value specifies the maximum mesh width reduction of the fluting sections. The valid range for this number is from 0 to 70. The default value is 0. Option only available if the Add Fluting checkbox is selected.
Z Elevation Multiplier:
Elevate the spiral on the Z Axis by this amount times the spiral radius. If this value is 0, a 2d Polyline is created, otherwise the polyline is a 3dPoly.
Spiral Rotation Step Factor:
This value alters the amount of rotational angle that’s applied to the spiral, dividing into the actual theta rotation angle value. A larger number limits the rotation, and a smaller number creates a larger rotation. And thus, a longer spiral. This number has to be greater than 0. The value can range from 1 to 200.
Uncoiling Factor:
The uncoiling factor affects the rate the spiral evolves from the Origin, (i.e. the spiral distance from the origin). A larger number uncoils the spiral faster. This value should be less than or equal to 1. Setting this number to an angle’s Co-Tangent value (as in the formula’s constant radial angle ‘a’) will create the spiral associated with that angular degree.
Mesh Width Factor:
This factor affects the size of the PolyFaceMesh. A larger number creates a larger mesh. This value should be less than 1
Depression Sections per Flute:
This value specifies the flute width in sections along which to apply the mesh flute reduction percentage. The value can range from 2 to 30. The default is 2. Option only available if the Add Fluting checkbox is selected.
Ridge Sections per Flute:
This value specifies the width of the flute ridge in sections that do not have a mesh reduction applied. The value can range from 1 to 200. The default is 1. Option only available if the Add Fluting checkbox is selected
Reset button:
This dialog button resets the dialog box parameters, and options to the initial dialog settings. Those values are: Number of Sections: 600 Points Per Section: 52 Spiral Direction: Clockwise Generate PolyFaceMesh: Checked Add Fluting: Not checked, enabled Percent Reduction: 0, and disabled Elevation (Z axis) Multiplier: 0.33 Spiral Rotation Step Factor: 20 Uncoiling Factor: 0.09 Mesh Width Factor: 0.33 Depression Sections per Flute: 2, and disabled Ridge Sections per Flute: 1, and disabled

 

3dSpiral, a 3d Equi-Angular Spiral Generator for AutoCAD

Licensed Versions available for AutoCAD 2000-2002;  2004-2006;  2007-2009  2010-2012;  2013-2014;  2015;  2016;  2017 (for 32, or 64bit)

 
 

ObjectARX 3d Equi-Angular Spiral Generator: $39.95 No Demo Version Available. For More Information - eMail With AutoCAD™ Version and (x32/x64) Platform.

 

More mathematical information on the equiangular spiral can be obtained from the following web sites:

http://en.wikipedia.org/wiki/Logarithmic_spiral

http://www.ee.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html#spiral

http://xahlee.org/SpecialPlaneCurves_dir/EquiangularSpiral_dir/equiangularSpiral.html

And of course, Chapter 11 ‘Equiangular Spiral’, ‘On Growth and Form (The Complete Revised Edition)’ by D’Arcy Wentworth Thompson, Dover Publications, ISBN 0-486-67135-6

http://www.amazon.com/exec/obidos/ASIN/0486671356/qid=978416497/sr=1-1/002-2136127-2613637

In addition there’s a newer book (it was new way back in 2000) I haven’t had a chance to check out that looks promising also, ‘The Algorithmic Beauty of Sea Shells’ by Hans Meinhardt, Springer Verlag; ISBN 3540639195:

http://www.amazon.com/exec/obidos/ASIN/3540639195/qid=979674949/sr=1-1/ref=sc_b_1/102-7679031-9804129

And the ancient mystery of the spiral form is discussed in this book:

The Mystic Spiral, Journey of the Soul  by Jill Purce

 

---

20 August 2016
 
info@henleygraphics.com
 

---